经典渗透率计算模型
两种经典的核磁共振渗透率估算模型为SDR和Timur/Coates模型。初期研究表明,碎屑岩的渗透率与束缚水饱和度相关,在此基础上,Coates 根据孔隙度和可动流体与束缚流体占比来确定渗透率。后续研究逐渐认识到T2特征值与渗透率具有相关关系,而T2与孔隙大小有关,Kenyon用孔隙度和T2几何平均值来确定渗透率。事实上,Timur/Coates模型和SDR模型都考虑了孔径分布对渗透率的影响,但Timur/Coates 模型认为渗透率只是可动流体和束缚流体的两段式贡献作用,而SDR模型将孔径分布简单平均化。图1为SDR和Timur/Coates模型示意图。
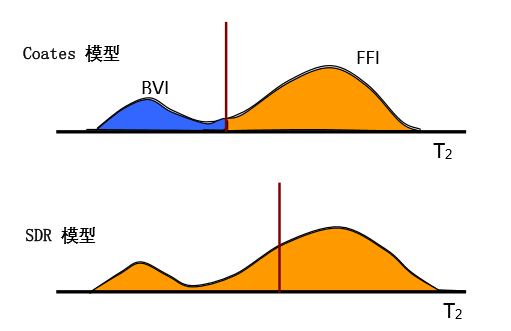
图1 核磁共振渗透率模型示意图
SDR模型
核磁测井能够很好的预测渗透率是因为T2弛豫时间与孔隙大小(或孔隙体积与表面积的比值)有关,即:
\[T_2\approx\frac{V}{\rho_2S}\]
并且能够提供预测渗透率的经验公式:
\[K=A(\varphi_{me})^C{({\overline{T}}_{2gm})}^B\]
式中,A为SDR模型渗透率乘积因子,与地层类型有关,单位mD,缺省值A=4mD; B为 SDR模型T2对数平均指数,缺省值B=2;C为SDR模型孔隙度指数,缺省值C=4。通常核磁共振测井是通过现场取心,进行实验室岩心实验,然后求取系数建立SDR模型来求取渗透率。
SDR模型利用T2分布的几何平均值来估算渗透率,是根据饱和盐水的岩石样品的实验结果建立的,通常对水层有较好的预测结果。对于油层,T2几何均值向自由流体T2偏移,估算的渗透率不正确。在原状气层,相对于冲洗过的气层,T2几何均值太低,渗透率相应偏低。由于烃对T2gm的影响不可校正,因此SDR模型对于含烃地层不适用。
Timur/Coates模型
多项研究表明,碎屑岩的渗透率与束缚水饱和度有关。NMR测量的有关物理量为束缚流体体积和自由流体体积。
\[K=A(\varphi_{me})^B\left(\frac{\varphi_{mf}}{\varphi_{mb}}\right)^C\]
式中,A为Timur/Coates模型渗透率乘积因子,单位mD,缺省值A=1mD;B为Timur/Coates模型孔隙度指数,缺省值B=4;C为Timur/Coates可动流体束缚流体比指数,取决于地层的沉积过程,对于每种地层都是不同的,缺省值C=2。
Timur/Coates模型用孔隙度、束缚水饱和度、自由流体指数来预测渗透率,因此当束缚水饱和度和孔隙度能够被准确地确定时,这就是一个较常用的方法。 经验表明,Coates模型比SDR模型更灵活。通过恰当的岩心刻度,可以应用于不同的地层和储层。只要毛管束缚流体孔隙度中不含任何烃的贡献,束缚流体体积就不受其他流体相的影响。
Coates模型、SDR模型是目前常用的核磁共振测井渗透率计算模型, 但同样存在应用局限性。 对于具有简单孔隙结构的常规储层岩心,两种方法对渗透率的表征结果较理想,但随着岩样孔隙空间越来越多样、孔径分布越来越复杂,它们很可能不太准确。对于具有孔隙跨尺度特征、孔喉分布较宽的储层,如同时发育孔、洞、缝的碳酸盐岩储层,或是发育大量纳米级孔隙的页岩储层,由于不同尺寸孔喉的连续分布且对渗透率的贡献差异较大,需要有针对性地修正和完善模型。下面对改进的经典渗透率计算模型进行简单介绍。
SDR模型改进
Amabeoku等人重新调整了SDR模型中的系数,使修正后的模型能够更加适用于碳酸盐岩渗透率的计算。2004年,Hassall等人认为宏观孔隙度 Vmacro会对碳酸盐岩渗透率造成影响,从而对SDR模型进行了改进:
\[K=K_{sdr}{(\varphi/(\varphi-V_{macro}))}^2\]
Chang等(1994)发现,如果将T2>750ms的孔隙度(多半是溶洞型孔隙度)排除在外,T2LM对数平均值公式对于渗透率预测效果很好。提出孤立孔洞模型:
\[K_{vuggy}=4.75\bullet(\varphi_{<\ 750})^4\bullet T_{2LM,<\ 750}^2\]
表面弛豫率与孔隙半径存在对应关系,基于Kozeny-Carman公式将其引入SDR模型中可更好地进行渗透率计算。表面弛豫率的计算成为了这类改进方法的难点,国内外学者多使用二维的核磁实验来对表面弛豫率进行计算。
Timur/Coates模型改进
Amabeoku等人对Timur/Coates模型的系数进行了调整,使得该模型能够更好地在碳酸盐岩储层中进行应用。Sigal则提出了一个新的特征衰减时间Tcoates,并利用该特征衰减时间将Timur-Coates公式转换成与SDR公式相同的形式。
\[T_{coates}=T_c(FFI/BVI)\]
\[K=CT_{coates}^2\varphi^4\]
Trevizan等人将Timur-Coates公式中的系数作出了修改,使该模型与渗透率的相关性得到了改善。
\[K=\left(\frac{\phi}{C}\right)^m\left(\frac{FFI}{BVI}\right)^n\left(\frac{T_{2gm}}{{FFI}^2}\right)^x\]
相关资料
- Amabeoku MO,Funk JJ,Al-dossary SM, et al. Calibration of Permeability Derived From Nmr Logs in Carbonate Reservoirs[C]//Spe-68085-ms, [S.l.]: Society of Petroleum Engineers, 2001: 11.
- Hassall J,Ferraris P,Al-raisi M, et al. Comparison of Permeability Predictors From Nmr, Formation Image and Other Logs in a Carbonate Reservoir[C]//Spe-88683-ms, [S.l.]: Society of Petroleum Engineers, 2004: 13.
- Sigal R. Coates and Sdr Permeability: Two Variations on the Same Theme[J]. Petrophysics, 2002, 43(1): 13.
- Lala AMS,El-sayed NAE. Calculating Absolute Permeability Using Nuclear Magnetic Resonance Models[J]. Arabian Journal of Geosciences, 2015, 8(10): 7955-7960.
